In December of 1875, Werner von Siemens, German electrical engineer and inventor (the person who founded the company currently called Siemens and makes toothbrushes etc) also performed an experiment to measure the speed of light. His contributions have been mostly forgotten (the HSC syllabus only mentions Fizeau, Focoult, Roemer, Bradley) and his records are very obscure. It is through the research of Bob Chen, tutorgum, that it’s been brought to light. The original German transcription and the English translation have been published at the bottom of this article.
For the record, I first discovered this experiment from this page: https://en.wikipedia.org/wiki/Speed_of_light
But there was no elaboration as to his actual experimental method. It is below!
In his paper, he talks about his original design and his revised design.
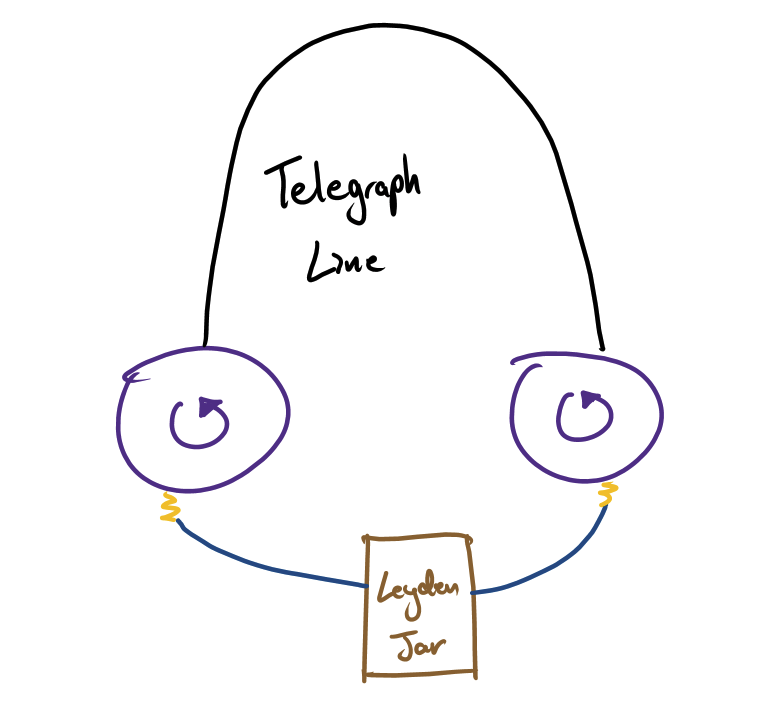
His initial experiment consisted of 2 identical large steel drums (diameter of 40mm) rotating at a high velocity (100 revolutions per second). These drums were connected to a telegraph line (like a telephone line but really old). The telegraph line was from Köpnik to Erkner, a distance of 12.68km one way.
When he connects the Leyden Jar, the electricity in the blue path sparks on the left-hand side, creating a spark mark on the left cylinder. The electricity them moves along the black path (telegraph wire) (which is also at the speed of light) which will take some time, and in this time, both cylinders are still rotating. By the time the electricity finally gets back to the right-hand side drum, it sparks again. This creates a second spark. He measured the angular separation of the 2 sparks, and hence because he knew the rotational velocity, he could calculate how much time elapsed between these 2 events. This time would be equal to the time taken to travel in the black wire.
By measuring the difference in distance, he could determine the velocity of light.
However, he laments in his paper that this method was not feasible because it’s too hard for the drums to be moving at exactly the same speed. He devises a new plan below:
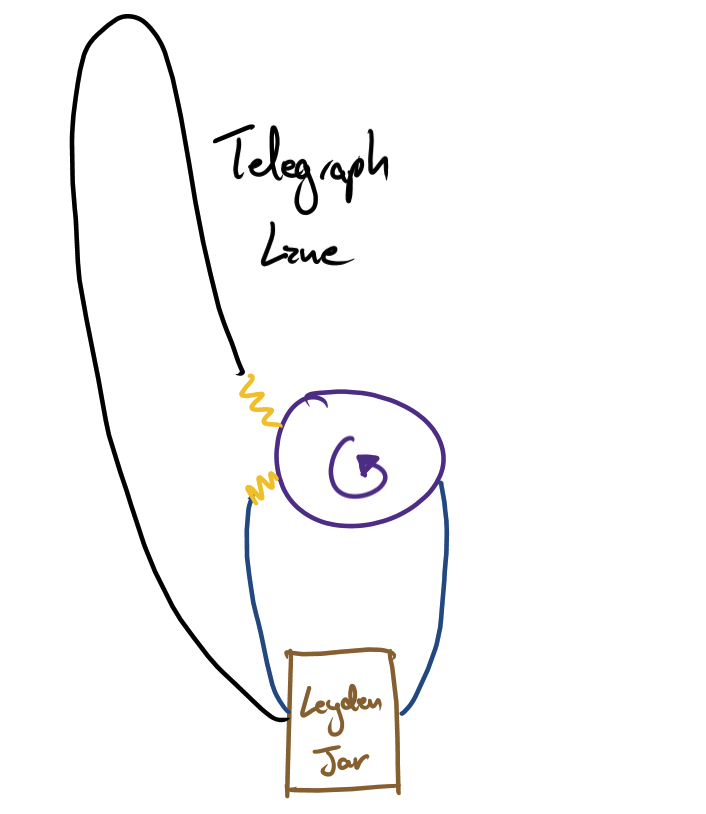
With this new methodology, he has the blue path, which is just a few centimeters. The black path is the telegraph.
First the electricity in the blue path sparks, creating a spark mark on the cylinder. The electricity in the black path must take a longer path, and in this time, the cylinder is still rotating. By the time the electricity finally gets back to the drum, it sparks again. This creates a second spark. He measured the angular separation of the 2 sparks, and hence because he knew the rotational velocity, he could calculate how much time elapsed between these 2 events. This time would be equal to the time taken to travel in the black wire.
He assumed the blue path to be so short that it’s basically instantaneous to simplify the calculations.
He used 2 different telegraph lines Sagan-Malmitz (11.686 km one way) and also Sagan-Streckenblock (3.676 km one way).
This served 3 purposes. First, it allowed him to verify that the delay for the black wire was truly due to the increase in path length and not some systematic error (what if it was because the telegraph transformer introduced delay).
It also allowed him to get more data points, and he can create a line of best fit to reduce the effect of random error.
Finally, he was worried about the capacitance effect. The long wires could act as capacitors – but their delay in the signal would be with the square of distance, but he observed a linear relationship indicating it was just the speed of light.
Appendix
Translated to english:
IX. Measurement of the Propagation Speed of Electricity in Suspended Wires;
by W. Siemens.
(From the Monthly Reports of the Academy, December 1875.)
The persistent frosty weather of last winter and the kind cooperation of the administration of the Lower Silesian-Marcher Railway, and particularly of its telegraph inspector Mr. Wehrhahn, made it possible for me to carry out a proposal I had already made in 1845 for the direct measurement of the propagation speed of electricity ¹). Unfortunately, the thaw weather that occurred during the experiments prevented their complete execution, but the results obtained already appear important enough to justify their communication before the
complete conclusion of this work.
The method I have used here differs in some essential points from my earlier proposal. According to the latter, the execution of the measurement required two steel cylinders, isolated from each other and from the ground, rotating uniformly, and two double wires, one of which connected the two
[Page 2]
cylinders, the other connecting two insulated points leading opposite the peripheries of the cylinders. If one discharged a Leyden jar between a point and its associated wire end, the discharge current had to pass through the entire circuit and leave a spark mark on the mantle of each of the two steel cylinders. The difference in the distances of these marks, produced during the rotation of the cylinders, from those produced in the same way with stationary cylinders, was then the measure of the time that electricity took to traverse half the circuit.
Considerable difficulties stood in the way of the execution of this plan. These consisted, firstly, in the difficulty of procuring four equally long, sufficiently well insulated wires originating from the same place, but mainly in the mechanical task of producing two steel cylinders, completely isolated from each other and from the ground, so lightweight and so perfectly centered, that the necessary speed of rotation of 100 to 150 revolutions per second could be given to them. I therefore applied a modified method in which only one, non-insulated, steel cylinder and only one double wire was required.
It is based on the application of two Leyden jars or charge plates, of which the inner coating of one is connected directly by a short wire, that of the other through the long circuit wire with the rotating, grounded cylinder near the opposing point. The outer, insulated coatings of the jars are metallically connected. If they are grounded, then at the same moment the electricity of the inner coating of both jars is released and discharges through the point and the rotating cylinder to ground. If the rotation is sufficiently fast and the wire long enough, two spatially separated marks are created on the cylinder, the distance between which is the
[Page 3]
measure of the time that electricity took to traverse the wire from the jar to the point.
I also modified this arrangement in such a way that instead of one point I placed two opposite the cylinder mantle, and connected one point directly to one, the other through the wire to the other jar. The points were placed as close together as possible, so that the marks produced simultaneously by both with a stationary cylinder were close together and, if possible, in a plane parallel to the axis. An discharge of the jars was then first made with the cylinder stationary, and only then the discharge used for measurement with the rotating cylinder. The apparatus itself was the same that I used for measuring the speed of projectiles in gun- or rifle barrels and described in other places.
The steel cylinder is made as light as possible, turned out of a solid steel cylinder. It has a diameter of 40 mm and a side height of 10 mm. Its steel axle is provided with a thread, into which the teeth of a ratchet wheel engage. This is uniformly rotated by a powerful clockwork with weight drive.
The speed of rotation of the cylinder can be adjusted within wide limits by a regulator, also described elsewhere, during rotation. The ratchet wheel, equipped with 100 teeth, carries a small nose, through which a light hammer is lifted after each revolution, which strikes a small bell. If the regulator is set so that the bell strokes coincide exactly with the pendulum strokes of a seconds pendulum, then the cylinder rotates exactly 100 times per second.
Opposite the cylinder wall, a magnifying glass with crosshairs is attached, which serves to read the angular distance of the spark marks.
[Page 4]
In the state of rest, a screw without end with a cut head can be brought into engagement with the cylinder by moving a lever, by which it can be slowly rotated until the thread of the magnifying glass passes through the center of the spark mark. In this way, millionths of a second can still be read accurately and 10 millionths estimated.
The conductive point opposite the cylinder mantle consists of a thin glass tube, into which a platinum wire as fine as possible is fused. After this glass tube is inserted into a metal tube with screw thread and the end of the same opposite the cylinder mantle is carefully ground hemispherical, it is screwed as close as possible to the rotating cylinder.
The glass sheath, which surrounds the platinum wire up to its outermost end, is intended to prevent sparks from taking a lateral direction. Very weak sparks leave a single bright point on a polished steel surface, stronger ones a bundle of sparks, in the middle of which the crosshairs must be set. In order to facilitate the finding of the spark marks, the cylinder is sooted in a known manner before use. Then every spark mark, even the weakest and barely visible to the naked eye, is surrounded by a clear ring-shaped halo, which makes it easy to bring them into the field of view of the microscope. Instead of Leyden jars, I usually used charge plates with tinfoil-covered mica sheets. These were carefully embedded in a resin compound so that they were able to hold the assumed charge for a longer time without noticeable weakening. They were equipped with a switch, which allowed them to be loaded separately from the point (or the two points, if two were used) simultaneously by a Holz’sche machine
[Page 5]
and then at the last moment before the experiment to connect the coatings, which had been connected to ground until then, with the respective point or points, while the conductive, connected other coatings ended in a gutta-percha insulated wire. The discharge was then brought about by driving a knife, conductively connected to ground, through the insulated wire by means of a strong hammer blow, thereby bringing about a short but as resistance-free discharge of the connected coatings to ground.
In this way, it was possible to completely eliminate the initially very disturbing, false discharge marks on the cylinder, caused by slow discharge of the charge plates.
With the apparatus thus distributed, a series of experiments were first carried out in the room. It was observed that the discharge of a jar in a discharge circuit of low resistance proceeds so quickly that the mark bundle on the rotating cylinder is not essentially different from that produced on a stationary cylinder. Isolated spark marks that are almost always found irregularly on the cylinder surface are obviously attributable to the so-called residuum of the charge plates. The phenomenon changes when the discharge takes place through very large resistances. In this case, a continuous series of spark marks is formed on the cylinder, but never a homogeneous line, which would correspond to a measurable time- lasting electric current. It cannot be concluded from this, however, that the total discharge, even in this case, consists of a series of partial discharges of immeasurably short duration.
If one imagines, on the contrary, that the discharge consists of a continuous current of decreasing strength, the spark would therefore be regarded as a continuous Davy’s arc lamp, then the occurrence of a series of spatially separated spark marks can still be explained.
[Page 6]
Namely, by the rotating cylinder mantle, the adjacent air layers are carried along, and indeed all the more completely, the closer the air layer is to the rotating cylinder surface. If one now assumes that the beginning of the discharge had broken through the air layer between the point and the cylinder rotating with the cylinder, thus creating a glowing, well-conducting channel between point and cylinder, then this channel is carried along by the rotation.
If there is now a continuous supply of electricity from the point, the channel is continuously lengthened from this, since, despite its greater length, it offers less resistance to electricity than the unbroken cold air that has inserted itself between point and cylinder wall.
However, once this discharge path has reached a certain length, its resistance becomes greater than that of the cold air between point and cylinder, a new breakthrough occurs and thus the formation of a new spark mark and discharge path.
The discharge of a jar through a rubber tube filled with water or through a wet cord around an immediately preceding series of fine spark marks, but there was no time loss to be observed for the beginning of the discharges.
Since it seemed probable to me for various reasons, especially also as a result of the results obtained by Fizeau and Gounelle, that the propagation speed of electricity must be proportional to the specific conductivity of the material, I repeated this experiment with a 100 foot long, 20 mm inner diameter rubber tube, which was filled with zinc vitriol solution. To my great surprise, however, no time difference was found here either between the direct discharge mark and the mark of the first partial discharge through the 100 foot long liquid tube. Since a difference of 5 millionths of a second would still have been reliably detectable, it is thus established that the propagation speed
[Page 7]
of electricity in liquids must be over 800 geographical miles per second.
Since the conductivity of copper is at least 200 million times greater than that of zinc vitriol solution, the speed of electricity in copper would have to be at least 160,000 million miles if the specific conductivity were synonymous with the speed of electricity.
It can hardly be assumed that electrolytic conductors conduct electricity faster than metals of equal conductivity; the opposite was more likely, since it must be assumed that molecular movements take place in electrolytic conduction.
In the experiments to be carried out with longer telegraph lines, the question should now be decided whether a certain measurable propagation speed is to be ascribed to the propagation speed of electricity, like to light, or whether the delay values measured by various observers are wholly or at least largely attributable to the delay of the current phenomenon at the distant end of the line due to the jar effect of the wire. To this end, the experiments should be carried out shortly one after the other with the most possible different wire lengths and each time the jar capacitance of these wire lengths should be measured.
The first experiments took place on February 23 of this year in Köpnik, whither Dr. Frölich, who carried out the following measurements both here and later in Sagan with his usual skill and care, had already gone beforehand with the apparatus. First, through a series of experiments, it was established that the insulation of the line was sufficient in the prevailing mild frosty weather to conduct the discharge spark through the telegraph line (made of 5 mm
[Page 8]
thick iron wire) leading to Erkner, 12.68 km away, and back to the rotating cylinder.
So the experiments were done with two points, i.e., one (smaller) jar was discharged directly through one point, the second considerably larger jar through the line and the other point.
Seven discharges were made. The readings taken the following day revealed:
122.8
111.7
125.3
142.7
117.6
121.8
134.3
on average 125.2 millionths of a second.
Since the outgoing and returning line was 2 × 12.68 = 25.36 kilometers, this results in a speed of 202,600 km or 27,300 geographical miles per second. It turned out here that the direct discharge spark of the small jar, passing through one point, always formed a small bundle of spark marks, surrounded by a larger closed halo, within which the soot was flung away, while a series of smaller spark marks was formed through the second point, which were surrounded by no or only a very weak halo. Often a faint point was also visible in the line of the last point, exactly opposite the local discharge mark. The same was either a consequence of a back or side discharge from the cylinder onto the adjacent point, or more likely an influence effect between the parts of the outgoing and returning line closest to the cylinder, fastened to the same poles. In general, the local discharge was far stronger than necessary, which had the disadvantage that the first line discharge point often still
[Page 9]
fell into the halo of the local discharge and was therefore difficult to recognize.
Due to the onset of thaw weather, in which the insulation of the telegraph lines is not sufficient for the conduction of frictional electricity, the further intended experiments were prevented for a longer time. When later frosty weather returned, Mr. Wehrhahn made available to us the double lines emanating from the Sagan station to Malmitz and a block section lying between Sagan and Malmitz. Dr. Frölich, who went to Sagan with the apparatus, succeeded in making two valuable series of observations. They were partly done with two, partly with one point. In these experiments, the double point always occurred, and Dr. Frölich convinced himself through a series of control experiments that this double or rather starting point had a local cause and could not originate from electricity that had traversed the entire line. The line discharges here form a rather long tail of 6 to 8 points, whose distance from each other was initially about 30, at the end 15 to 20 millionths of a second, and which was often followed by a short line without clear points. This harmonizes very well with the above explanation of the occurrence of discharge points in continuous discharge. The stronger the discharge current, the longer the discharge channel is maintained on the periphery of the rotating cylinder, the further apart the points must therefore also be. If the discharge is nearly completed, the current strength and heat development are so weak that no discharge channel can be maintained at all, and the point series therefore transitions into a weak line.
First, the double line from Sagan to the 11.686 km distant Malmitz was used. The reading of 22 discharges revealed:
[Page 10]
| 100,4 | 88,7 | 108,7 | 104,2 |
| 102,7 | 103,6 | 101,1 | 104,2 |
| 91,2 | 95,6 | 108,3 | 107,3 |
| 100,8 | 97,5 | 102,0 | 110,3 |
| 100,6 | 100,5 | 104,2 | |
| 91,4 | 104,7 | 102,5 |
on average 101.4 millionths of a second. Since the distance traversed was 2 × 11.686 km = 23.372 km, the speed was 230,500 km = 31,060 geographical miles.
The next double line switched on, 3.676 km long, Sagan-Streckenblock, yielded 12 discharges:
| 39.4 | 23.0 |
| 41.9 | 25.9 |
| 27.8 | 30.5 |
| 27.0 | 22.1 |
| 35.6 | 28.9 |
| 28.4 | 34.8 |
on average 30.4 millionths of a second. This results in a speed of 241,800 km = 32,590 geographical miles.
A next series of 13 discharges with one point, to which Dr. Frölich gives less confidence, because the regulation of the clockwork was less carefully executed, gave:
| 87.8 | 78.2 | 80.8 |
| 84.5 | 96.3 | 96.3 |
| 76.4 | 93.1 | 93.5 |
| 93.2 | 85.5 | 101.2 |
| 117.9 |
on average 91.1 millionths of a second, thus a speed of 256,600 km or 34,580 geographical miles.
Even if these measurements do not yet yield the degree of agreement that is to be expected from the method and which will also be achieved in a repetition of the experiments under favorable circumstances, they nevertheless clearly show that the propagation of
[Page 11]
electricity in conductors occurs with a certain speed, independent of the length of the conductor, which lies between 30 and 35,000 miles per second in iron wires.
I am inclined, in light of these experiments, as a result of the results obtained with the rubber tube, to the view that the actual speed of electricity is immeasurably great and that the delays found by Wheatstone (Pogg. Ann. Vol. 34, p. 464), Fizeau and others are entirely based on the jar effect of the overhead lines. If this were the case, then the almost 3 times longer Sagan-Malmitz line would have had to show an approximately 9 times greater delay than the Sagan-Streckenblock line, while the speed, according to the experiments carried out under the same conditions with double points, was in the ratio of 31:32.6. But even apart from these numbers contradicting the quadratic delay law, the delay is generally far too great to be explained by charge delay alone. The jar capacitance of the two lines was measured by Dr. Frölich with the continuous rocker according to the method previously used by me to determine the charge laws ¹) measured. The measurement revealed:
For Sagan-Malmitz:
Galvanometer in charge circuit 0.181 in discharge circuit 0.120 on average 0.1505
For Sagan-Streckenblock:
Galvanometer in charge circuit 0.066 in discharge circuit 0.061 on average 0.0635 which on average gives a jar capacitance of the overhead line of 5 mm wire thickness of 0.053 m.f. per mile.
As a unit of capacitance, the so-called microfarad (m.f.) introduced in cable technology, derived from Weber’s absolute unit of Pogg. Ann. Vol. 102, p. 66.
- Pogg. Ann. Bd. 102, S. 66.
[Page 12]
quantity of electricity, is assumed. For direct comparison of the measured delay values with those which must result as a consequence of the charging of the wires, the delay measurements can serve, which Dr. Serie carried out in my laboratory with the help of an artificial cable, i.e., a series of 32 capacitors of approx. 20 m.f. each, which were connected to each other by resistors of 550 Q.E. each.
- The measurements were made with my uncommonly sensitive electrodynamic (iron-free) relay and a chemical recording telegraph with double needles. 32 sections of the cable cabinet were switched on. They represented a resistance of 17600 Q. E. = W and a capacitance of 639.6 m. f. = C. This resulted in a delay of 0.72 sec., thus per million of the product resistance × capacitance (W. C.) of 0.0640 sec.
- 24 sections switched on.
W = 13200 Q. E.
C = 483.9 m. f.
resulted in delay 0.45 sec.
per million W C. 0.0715
3. 16 sections
W = 8800
C = 319.6 m. f.
resulted in delay 0.22
per million W C. 0.078 sec.
This gives on average a delay for 1 million
W C. of 0.0712 sec.
Since the Sagan-Malmitz line and back, according to the measurement carried out by Dr. Frölich, has a
capacitance C = 0.151 m. f.
Resistance W = 189.0 Q. E.
therefore WC=28.5;
according to this, the jar effect, assuming
[Page 13]
the quadratic law, could only have caused a delay of 2.0 millionths of a second, while it could only be 0.3 millionths of a second for the Sagan-Streckenblock line.
If one also considers that these delay times would have to be significantly greater than in the cable measurements, because more time elapsed until the electrical potential of the spark-emitting point was so great that the spark could jump to the cylinder, it is nevertheless evident that, for example, the delay of 30.4 millionths of a second measured on the Sagan-Streckenblock section must be of a different origin than the jar delay of 0.3 millionths of a second calculated. I hope to find the opportunity in the course of this winter, not only to repeat the above experiments under better conditions and with improved devices, but also to extend them to a copper line, in order to decide by direct measurements the question whether the speed of electricity depends on the nature of the metallic conductor or not. According to the experiments carried out with the metallic zinc vitriol solution-filled rubber tube, the latter appears probable to me. Kirchhoff, based on Weber’s fundamental law for the motion of electricity, found the number 41,000 miles for the speed of electricity in conductors by calculation and came to the result that this speed must be the same in all conductors.
Our measurements at least come much closer to Kirchhoff’s value than to that of Wheatstone, estimated from the lagging of the middle spark, of 61,900 geographical miles. Fizeau and Gounelle, with the help of their differential measurement method for galvanic currents in telegraph lines, found 17,792 km for copper and 10,1710 km for iron, thus for iron only about half as great a speed as our measurements have yielded.
[Page 14]
Even lower speed values have been found by Walker, Mitchell, and Gould on American telegraph lines with electromagnetic recording instruments, the latter even only 12,851 English miles. However, no great weight is to be placed on these measurements, since the inertia of the electromagnetic instruments is too great and uneven for the measurement of such small time fractions. The measurements of Fizeau and Gounelle appear to be of far greater weight. They have not been able to take into account the delaying influence of the charge, to which I only drew attention after their experiments were conducted, and the necessary data are also lacking in the description of their experiments to be able to calculate the charge delay retrospectively. Even if the charge delay, due to the relatively large length of their line (approx. 300 km), should be over 1000 times greater than in my experiments, it is still not sufficient to explain the difference. I therefore believe that the difference in the speed of electricity in iron and copper found by Fizeau is also not yet to be regarded as established.
ORIGINAL GERMAN
This is the original German (originally sourced from here):
IX. Messung der Fortpflanzungsgeschwindigkeit
der Elektricität in suspendirten Drähten;
von W. Siemens.
(Aus den Monatsberichten der Akademie, December 1875.)
Das andauernde Frostwetter des letzten Winters und
das freundliche Entgegenkommen der Verwaltung der
Niederschlesisch-Märkischen Eisenbahn, und namentlich
ihres Telegraphen-Inspectors Hrn. Wehrhahn, machten
es mir möglich, einen schon im Jahre 1845 von mir ge-
machten Vorschlag zur directen Messung der Fortpflan-
zungsgeschwindigkeit der Elektricität ¹) in Ausführung zu
bringen. Leider verhinderte das während der Versuche
eintretende Thauwetter die vollständige Durchführung der-
selben, doch erscheinen die erhaltenen Resultate schon
wichtig genug, um ihre Mittheilung vor völligem Ab-
schlusse dieser Arbeit zu rechtfertigen.
Die von mir hierbei zur Anwendung gebrachte Me-
thode weicht in einigen wesentlichen Punkten von meinem
früheren Vorschlage ab. Nach diesem bedurfte es zur
Ausführung der Messung zweier von einander und vom
Erdboden isolirter, gleichmäſsich rotirender Stahlcylinder
und zweier Doppelleitungen, von denen die eine die bei-
[Page 2]
den Cylinder, die andere zwei isolirte Spitzen leitend ver-
band, welche den Peripherien der Cylinder nahe gegen-
über standen. Entlud man eine Leydener Flasche zwischen
einer Spitze und dem ihr zugehörigen Drahtende, so muſste
der Entladungsstrom den ganzen Leitungskreis durchlaufen
und auf dem Mantel jedes der beiden Stahlcylinder eine
Funkenmarke zurücklassen. Die Differenz der Abstände
dieser während der Rotation der Cylinder erzeugten Mar-
ken von denen in gleicher Weise bei ruhenden Cylindern
hervorgebrachten, war dann das Maaſs der Zeit, welche
die Elektricität zum Durchlaufen des halben Kreislaufes
gebrauchte.
Der Ausführung dieses Planes standen erhebliche
Schwierigkeiten entgegen. Diese bestanden einmal in der
Schwierigkeit, vier gleich lange, von demselben Orte aus-
gehende, hinlänglich gut isolirte Leitungen zu beschaffen,
hauptsächlich aber in der mechanischen Aufgabe, zwei von
einander und vom Erdboden völlig isolirte Stahlcylinder
so leicht herzustellen und so vollkommen zu centriren,
daſs ihnen die nöthige Umdrehungsgeschwindigkeit von
100 bis 150 Umdrehungen in der Secunde gegeben wer-
den konnte. Ich wandte daher eine veränderte Methode
an, bei welcher nur ein, nicht isolirter, Stahlcylinder und
nur eine Doppelleitung erforderlich war.
Sie beruht auf der Anwendung zweier Leydener Fla-
schen oder Ladungstafeln, von denen die innere Belegung
der einen direct durch einen kurzen Draht, die der an-
deren durch die lange Kreisleitung mit dem rotiren-
den, zur Erde abgeleiteten, Cylinder nahe gegenüber-
stehenden Spitze verbunden ist. Die äuſseren, isolirten
Belegungen der Flaschen sind metallisch verbunden. Wer-
den sie zur Erde abgeleitet, so wird in demselben Momente
die Elektricität der inneren Belegung beider Flaschen frei
und entladet sich durch die Spitze und den rotirenden
Cylinder zur Erde. Ist die Rotation hinlänglich geschwind
und die Leitung lang genug, so entstehen auf dem Cylin-
der zwei räumlich getrennte Marken, deren Abstand das
[Page 3]
Maaſs der Zeit ist, welche die Elektricität zum Durchlaufen
der Drahtleitung von der Flasche zur Spitze gebrauchte.
Ich modificirte diese Anordnung auch in der Weise,
daſs ich anstatt einer Spitze deren zwei dem Cylinderman-
tel gegenüberstellte und die eine Spitze direct mit der
einen, die andere durch die Leitung mit der anderen
Flasche verband. Die Spitzen wurden möglichst nahe ne-
beneinander gestellt, so daſs die gleichzeitig von beiden
bei ruhendem Cylinder hervorgebrachten Marken dicht
beisammen und möglichst in einer mit der Axe paralle-
len Ebene lagen. Es wurde dann zuerst eine Entladung
der Flaschen bei ruhendem Cylinder und darauf erst die
zur Messung dienende Entladung bei rotirendem Cylinder
gemacht. Der Apparat selbst war derselbe, den ich zur
Messung der Geschwindigkeit der Geschosse im Geschütz-
oder Gewehrlaufe benutzt und an anderen Orten beschrie-
ben habe. Der Stahlcylinder ist möglichst leicht aus einem
massiven Stahlcylinder ausgedreht. Er hat einen Durch-
messer von 40 Mm. und eine Seitenhöhe von 10 Mm.
Seine Stahlaxe ist mit einem Gewinde versehen, in wel-
ches die Zähne eines Steigrades eingreifen. Dies wird
durch ein kräftiges Laufwerk mit Gewichtsbetrieb gleich-
mäſsich gedreht. Die Geschwindigkeit der Drehung des
Cylinders läſst sich durch einen ebenfalls anderweitig be-
schriebenen Regulator während der Rotation beliebig in-
nerhalb weiter Gränzen abändern. Das mit 100 Zähnen
versehene Steigrad trägt eine kleine Nase, durch welche
nach jeder Umdrehung ein leichter Hammer gehoben wird,
der an eine kleine Glocke schlägt. Wenn der Regulator
so eingestellt ist, daſs die Glockenschläge mit den Pen-
delschlägen eines Secundenpendels genau zusammen fallen,
so rotirt der Cylinder genau 100 Mal in der Secunde.
Der Cylinderwand gegenüber befindet sich eine Lupe mit
Fadenkreuz befestigt, welche zur Ablesung des Winkel-
abstandes der Funkenmarken dient.
[Page 4]
Im Zustande der Ruhe kann durch Bewegung eines
Hebels eine Schraube ohne Ende mit geschnittenem Kopfe
mit dem Cylinder in Eingriff gebracht werden, durch
welche dieser so lange langsam gedreht werden kann, bis
der Faden der Lupe durch die Mitte der Funkenmarke
geht. Es können auf diese Weise Milliontel Secunden
noch genau abgelesen und 10 Millionstel geschätzt werden.
Die dem Cylindermantel gegenüberstehende leitende
Spitze besteht aus dünnem Glasrohre, in welches
ein möglichst feiner Platindraht eingeschmolzen ist. Nach-
dem dies Glasrohr in ein Metallrohr mit Schraubengewinde
eingefuttert und das dem Cylindermantel gegenüberstehende
Ende desselben sorgfältig halbkugelförmig abgeschliffen
ist, wird es so nahe wie möglich an den rotirenden Cylinder
herangeschraubt.
Durch die Glashülle, welche den Platindraht bis zu
seinem äuſsersten Ende umgiebt, soll verhindert werden,
daſs Funken eine seitliche Richtung einschlagen. Sehr
schwache Funken hinterlassen auf einer polirten Stahl-
fläche einen einzelnen hellglänzenden Punkt, stärkere ein
Bündel von Funken, auf dessen Mitte das Fadenkreuz
eingestellt werden muſs. Um das Auffinden der Funken-
marken zu erleichtern, wird der Cylinder vor dem Ge-
brauche in bekannter Weise beruſst. Es ist dann jede,
auch die schwächste und mit bloſsem Auge kaum sicht-
bare Funkenmarke mit einem deutlichen ringförmigen Hofe
umgeben, der es ermöglicht sie leicht in das Gesichts-
feld des Mikroskopes zu bringen. Anstatt der Leydener
Flaschen benutzte ich in der Regel Ladungstafeln mit
Staniol belegten Glimmerblättern. Dieselben wurden sorg-
fältig in eine Harzmasse eingeschmolzen, so daſs sie im
Stande waren, die angenommene Ladung längere Zeit ohne
merkliche Schwächung festzuhalten. Sie waren mit einem
Umschalter versehen, welcher gestattete, sie getrennt von
der Spitze (oder den beiden Spitzen, wenn deren zwei be-
nutzt wurden) gleichzeitig durch eine Holz’sche Maschine
[Page 5]
zu laden und dann im letzten Momente vor dem Versuche
die bis dahin mit der Erde verbundenen Belegungen mit
der oder den respectiven Spitzen zu verbinden, während
die leitenden verbundenen anderen Belegungen in einem mit
Guttapercha isolirten Drahte endeten. Die Entladung
wurde dann dadurch bewirkt, daſs ein mit der Erde lei-
tend verbundenes Messer mittelst eines kräftigen Hammer-
schlages durch den isolirten Draht getrieben und dadurch
eine kurze aber möglichst widerstandslose Ableitung der
verbundenen Belegungen zur Erde herbeigeführt wurde.
Auf diese Weise gelang es, die anfänglich sehr störenden,
durch langsame Entladung der Ladungstafeln hervorgeru-
fenen, falschen Entladungsmarken auf dem Cylinder völlig
zu beseitigen.
Mit dem so verbreiteten Apparate wurden nun fürs
Erste im Zimmer eine Reihe von Versuchen angestellt.
Es wurde constatirt, daſs die Entladung einer Flasche in
einem Entladungskreise von geringem Widerstand so schnell
verläuft, daſs das Markenbündel auf dem rotirenden Cy-
linder nicht wesentlich verschieden von dem auf ruhendem
Cylinder erzeugten. Vereinzelte Funkenmarken, die
sich fast immer ohne Regelmäſsigkeit auf der Cylinder-
fläche finden, sind offenbar dem sogenannten residuum der
Ladungstafeln zuzuschreiben. Die Erscheinung ändert
sich, wenn die Entladung durch sehr groſse Widerstände
stattfindet. In diesem Falle bildet sich auf dem Cylinder
eine continuirliche Reihe von Funkenmarken, niemals aber
ein homogener Strich, welcher einem eine meſsbare Zeit
andauernden elektrischen Strome entsprechen würde. Es
ist aber hieraus nicht zu schliessen, daſs die Gesamt-
entladung auch in diesem Falle aus einer Reihe von Par-
tialentladungen von unmeſsbar kurzer Dauer bestehe.
Denkt man sich im Gegentheil, die Entladung bestände
aus einem continuirlichen Strome von abnehmender Stärke,
der Funken wäre mithin als andauernder Davy’scher
Lichtbogen aufzufassen, so läſst sich dennoch dies Auf-
treten einer Reihe von räumlich getrennten Funkenmarken
erklären.
[Page 6]
Durch den rotirenden Cylindermantel werden nämlich
die nächsten Luftschichten mit fortgerissen und zwar um
so vollständiger, je näher die Luftschicht der rotirenden
Cylinderfläche ist. Nimmt man nun an, der Beginn der
Entladung hätte die mit dem Cylinder rotirende Luftschicht
zwischen der Spitze und dem Cylinder durchbrochen, also
einen glühenden, gut leitenden Canal zwischen Spitze und
Cylinder hergestellt, so wird dieser Canal durch die Ro-
tation mit fortgeführt. Findet nun ein continuirlicher
Nachschub von Elektricität von der Spitze aus statt, so
wird der Canal von dieser aus continuirlich verlängert,
da er trotz gröſserer Länge der Elektricität geringeren
Widerstand darbietet, wie die undurchbrochene kalte Luft,
die sich zwischen Spitze und Cylinderwand eingeschoben
hat. Hat diese Entladungsstraſse jedoch eine gewisse
Länge erreicht, so wird ihr Widerstand gröſser wie der
der kalten Luft zwischen Spitze und Cylinder, es findet
ein neuer Durchbruch und damit die Bildung einer neuen
Funkenmarke und Entladungsstraſse statt.
Die Entladung einer Flasche durch ein mit Wasser
gefülltes Kautschukrohr oder durch eine nasse Schnur um
ehe umgehende Serie von feinen Funkenmarken, es war aber
kein Zeitverlust für den Beginn der Entladungen zu con-
statiren. Da es mir aus manchen Gründen, namentlich
auch in Folge der von Fizeau und Gounelle erhaltene-
nen Resultate, als wahrscheinlich erschien, daſs die Fort-
pflanzungsgeschwindigkeit der Elektricität der specifischen
Leitungsfähigkeit der Materie proportional seyn müſse, so
wiederholte ich diesen Versuch mit einem 100 Fuſs langen,
20 Mm. im lichten starken Kautschukrohre, welches mit
Zinkvitriolösung gefüllt war. Zu meiner groſsen Ueber-
raschung war aber auch hier keine Zeitdifferenz zwischen
der directen Entladungsmarke und der Marke der ersten
Partialentladung durch das 100 Fuſs lange Flüssigkeits-
rohr aufzufinden. Da eine Differenz von 5 Milliontheil
Secunde noch sicher zu erkennen gewesen wäre, so ist
hierdurch constatirt, daſs die Fortpflanzungsgeschwindig-
[Page 7]
keit der Elektricität in Flüssigkeiten über 800 geogr. Mei-
len per Secunde betragen muſs.
Da nun die Leitungsfähigkeit des Kupfers mindestens
200 Millionenmal gröſser ist wie die der Zinkvitriolösung,
so müſste die Geschwindigkeit der Elektricität in Kupfer
mindestens 160000 Millionen Meilen betragen, wenn die
specifische Leitungsfähigkeit mit Geschwindigkeit der Elek-
tricität gleichbedeutend wäre.
Daſs elektrolytische Leiter die Elektricität schneller
wie Metalle von gleicher Leitungsfähigkeit leiten sollten,
wird kaum angenommen werden können; es war das
Gegentheil wahrscheinlicher, da angenommen werden muſs,
daſs bei der elektrolytischen Leitung Molecularbewegungen
stattfinden.
Bei den mit längeren Telegraphenleitungen auszuführenden
Versuchen sollte nun die Frage entschieden werden,
ob die Fortpflanzungsgeschwindigkeit der Elektricität wie
dem Lichte ein bestimmte meſsbare Fortpflanzungsge-
schwindigkeit zuzuschreiben sey, oder ob die von ver-
schiedenen Beobachtern gemessenen Verzögerungswerthe
ganz oder doch zum groſsen Theile der Verzögerung
der Stromerscheinung am entfernten Leitungsende durch
Flaschenladung des Drahtes zuzuschreiben seyen. Zu dem
Ende sollten die Versuche kurz nach einander mit mög-
lichst verschiedenen Drahtlängen angestellt und jedesmal
die Flaschencapacität dieser Drahtlängen gemessen werden.
Die ersten Versuche fanden am 23. Februar dieses
Jahres in Köpnik statt, wohin Hr. Dr. Frölich, der die
nachfolgenden Messungen sowohl hier wie später in Sagan
mit gewohnter Geschicklichkeit und Sorgfalt ausgeführt
hat, schon vorher mit den Apparaten gegangen war.
Zunächst wurde durch eine Reihe von Versuchen con-
statirt, daſs die Isolation der Leitung bei dem obwalten-
den milden Frostwetter ausreichte, um den Entladungs-
funken durch die ganze nach dem 12,68 Kilom. entfernten
Erkner und zurück führende Telegraphenleitung (aus 5 Mm.
[Page 8]
dickem Eisendrahte) hindurch zum rotirenden Cylinder zu
leiten.
Also die Versuche wurden mit zwei Spitzen gemacht, d. h.
also, es wurde die eine (kleinere) Flasche direct durch die
eine Spitze, die zweite beträchtlich gröſsere Flasche durch
die Leitung und die andere Spitze entladen. Es wurden
sieben Entladungen gemacht. Die am folgenden Tage ge-
machten Ablesungen ergaben:
122,8
111,7
125,3
142,7
117,6
121,8
134,3
im Mittel 125,2 Milliontel Secunden.
Da die hin- und zurückgehende Leitung 2 × 12,68 = 25,36
Kilometer betrug, so ergiebt dies eine Geschwindigkeit
von 202600 Km. oder 27300 geogr. Meilen in der Se-
cunde. Es stellte sich hierbei heraus, daſs der durch die
eine Spitze gehende directe Entladungsfunke der kleinen
Flasche stets einen kleinen Büschel von Funkenmarken
bildete, umgeben von einem grösseren geschlossenen Hofe,
innerhalb dessen der Ruſs fortgeschleudert war, während
durch die zweite Spitze eine Serie von kleineren Funken-
marken gebildet wurde, die von keinem oder doch nur
einem sehr schwachen Hofe umgeben waren. Häufig
war in der Linie der letzten Spitze, genau gegenüber
der Lokal-Entladungsmarke, ebenfalls ein schwacher
Punkt sichtbar. Derselbe war entweder Folge einer
Rück- oder Seitenentladung vom Cylinder auf die benach-
barte Spitze, oder wahrscheinlicher eine Influenzwirkung
zwischen den zunächst dem Cylinder liegenden Theilen
an derselben Stangen befestigten hin- und rückkehrenden
Leitung. Im Allgemeinen war die Local-Entladung
weit stärker wie nothwendig, was den Nachtheil mit sich
führte, daſs der erste Linienentladungspunkt häufig noch
[Page 9]
in den Hof der Local-Entladung fiel und dadurch schwer
zu erkennen war.
Durch eintretendes Thauwetter, bei welchem die Iso-
lation der Telegraphenlinien für Fortleitung von Reibungs-
electricität nicht genügend ist, wurden die weiteren beab-
sichtigten Versuche für längere Zeit verhindert. Als später
wieder Frostwetter eintrat, wurden uns von Hrn. Wehr-
hahn die von der Station Sagan ausgehenden Doppellinien
nach Malmitz und einem zwischen Sagan und Mal-
mitz liegenden Streckenblock zur Verfügung gestellt. Es
gelang Hrn. Dr. Frölich, der sich mit den Apparaten
nach Sagan begab, zwei werthvolle Beobachtungsreihen
zu machen. Sie wurden zum Theil mit zwei, zum Theil mit
einer Spitze gemacht. Es trat bei diesen Versuchen der
Doppelpunkt stets auf und Hr. Dr. Frölich überzeugte
sich durch eine Reihe von Controlversuchen, daſs dieser
Doppel- oder vielmehr Anfangspunkt eine locale Ursache
hatte und nicht von Elektricität herrühren konnte, welche
die ganze Leitung durchlaufen hatte. Die Linien-Entla-
dungen bilden hier einen ziemlich langen Schweif von 6
bis 8 Punkten, deren Abstand von einander anfangs etwa
30, am Ende 15 bis 20 Milliontel Secunden betrug und
dem häufig ein kurzer Strich ohne deutliche Punkte folgte.
Es harmonirt dies recht gut mit der obigen Erklärung
des Auftretens von Entladungspunkten bei continuirlicher
Entladung. Je stärker der Entladungsstrom ist, desto
länger erhält sich der Entladungskanal auf der Peripherie
des rotirenden Cylinders, desto weiter müſsen also auch
die Punkte auseinander liegen. Ist die Entladung nahe
vollendet, so sind Stromstärke und Wärmeentwicklung
so schwach, daſs sich gar kein Entladungskanal mehr er-
halten kann, die Punktreihe mithin in einen schwachen
Strich übergeht.
Es wurde zuerst die Doppellinie von Sagan bis zum
11,686 Km. entfernten Malmitz benutzt. Die Ablesung
von 22 Entladungen ergab:
[Page 10]
100,4 88,7 108,7 104,2
102,7 103,6 101,1 104,2
91,2 95,6 108,3 107,3
100,8 97,5 102,0 110,3
100,6 100,5 104,2
91,4 104,7 102,5
im Mittel 101,4 Milliontel Secunden. Da der durch-
laufene Weg 2 × 11,686 Km. = 23,372 Km. lang war, so
war die Geschwindigkeit 230500 Km. = 31060 geogr.
Meilen.
Die demnächst eingeschaltete 3,676 Km. lange Doppel-
linie Sagan-Streckenblock ergab 12 Entladungen:
39,4 23,0
41,9 25,9
27,8 30,5
27,0 22,1
35,6 28,9
28,4 34,8
im Mittel 30,4 Milliontel Secunden. Es ergiebt dies
eine Geschwindigkeit von 241800 Km. = 32590 geogr.
Meilen.
Eine demnächst angestellte Serie von 13 Entladungen
mit einer Spitze, welcher Dr. Frölich weniger Zutrauen
schenkt, da die Regulirung des Laufwerks weniger sorg-
fältig ausgeführt war, gab:
87,8 78,2 80,8
84,5 96,3 96,3
76,4 93,1 93,5
93,2 85,5 101,2
117,9
im Mittel 91,1 Milliontel Secunden, mithin eine Geschwin-
digkeit von 256600 Km. oder 34580 geogr. Meilen.
Wenn diese Messungen auch noch nicht den Grad von
Uebereinstimmung ergeben, der von der Methode zu er-
warten ist und der auch bei einer Wiederholung der Ver-
suche unter günstigen Umständen erzielt werden wird, so
ergeben sie doch zur Evidenz, daſs die Fortbewegung der
[Page 11]
Elektricität in Leitern mit einer bestimmten, von der
Länge der Leiter nicht abhängigen, Geschwindigkeit ge-
schieht, die in Eisendrähten zwischen 30 und 35000 Meilen
per Secunde liegt. Ich neige mich vor diesen Versuchen,
in Folge der mit dem Kautschukrohre erhaltenen Resul-
tate, der Ansicht zu, daſs die wirkliche Geschwindigkeit
der Elektricität unmeſsbar groſs sey und daſs die durch
Wheatstone (Pogg. Ann. Bd. 34, S. 464), Fizeau und
Andere gefundenen Verzögerungen gänzlich auf Flaschen-
wirkung der oberirdischen Leitungen begründet wären.
Wenn dem so wäre, so müſste die fast 3 mal so lange
Leitung Sagan-Malmitz eine etwa 9 mal gröſsere Verzöge-
rung ergeben haben, wie die Leitung Sagan-Streckenblock,
während die Geschwindigkeit nach den unter gleichen Be-
dingungen angestellten Versuchen mit Doppelspitzen sich
wie 31 : 32,6 verhielt. Doch auch abgesehen von diesen,
den quadratischen Verzögerungsgesetze widersprechenden
Zahlen ist die Verzögerung überhaupt viel zu groſs, um
durch Ladungsverzögerung erklärt werden zu können. Die
Flaschencapacität der beiden Leitungen wurde von Hrn.
Dr. Frölich mit der continuirlichen Wippe nach der
früher von mir zur Ermittelung der Ladungsgesetze be-
nutzten Methode ¹) gemessen. Die Messung ergab:
Für Sagan-Malmitz
Galvanometer im Ladungskreise 0,181
im Entladungskreise 0,120
im Mittel 0,1505
Für Sagan-Streckenblock:
Galvanometer im Ladungskreise 0,066
im Entladungskreise 0,061
im Mittel 0,0635
was im Mittel eine Flaschencapacität der oberirdischen
Leitung von 5 Mm. Drahtstärke von 0,053 m. f. pro Meile
ergiebt.
Als Einheit der Capacität ist das in der Kabeltechnik
eingeführte, aus der Weber’schen absoluten Einheit der
- Pogg. Ann. Bd. 102, S. 66.
[Page 12]
Elektricitätsmenge abgeleitete sogenannte Microfarad (m. f.)
angenommen.
Zum directen Vergleichung der gemessenen Verzöge-
rungswerthe mit denjenigen, welche sich als Folge der
Ladung der Drähte herausstellen müſsen, können die Ver-
zögerungsmessungen dienen, welche Hr. Doctor Serie mit
Hülfe eines künstlichen Kabels, d. h. einer Serie von 32
Condensern à ca. 20 m. f., die durch Widerstände von je
550 E. untereinander verbunden waren, in meinem Laboratorio
angestellt hat.
Die Messungen geschahen mit meinem ungemein emp-
findlichen elektrodynamischen (eisenfreien) Relais und
einem chemischen Schreibtelegraphen mit Doppelnadeln.
- 32 Abtheilungen des Kabelschranks wurden ein-
geschaltet. Sie repräsentirten einen Widerstand
von 17600 Q. E. = W und eine Capacität von
639,6 m. f. = C. Es ergab sich eine Verzögerung
von 0,72 Sec. also pro Million des Productes Wider-
stand × Capacität (W. C.) von 0,0640 Sec. - 24 Abtheilungen eingeschaltet.
W = 13200 Q. E.
C = 483,9 m. f.
ergaben Verzögerung 0,45 Sec.
pro Million W C. 0,0715 - 16 Abtheilungen
W = 8800
C = 319,6 m. f.
ergaben Verzögerung 0,22
pro Million W C. 0,078 Sec.
Es giebt dies im Mittel eine Verzögerung für 1 Million
W C. von 0,0712 Sec.
Da die Leitung Sagan-Malmitz und zurück nach der
von Hrn. Dr. Frölich ausgeführten Messung eine
Capacität C = 0,151 m. f.
Widerstand W = 189,0 Q. E.
hiernach könnte durch die Flaschenladung, unter Annahme
[Page 13]
des quadratischen Gesetzes, nur eine Verzögerung von
2,0 Milliontel Secunden herbeigeführt seyn, während sie
für die Linie Sagan-Streckenblock nur 0,3 Milliontel
Secunden betragen könnte.
Zieht man nun auch in Betracht, daſs diese Verzöge-
rungszeiten wesentlich gröſser ausfallen müſsten, wie bei
den Kabelmessungen, weil längere Zeit verging, bis das
elektr. Potential der Funkengebenden Spitze so groſs war,
daſs der Funke zum Cylinder überspringen konnte, so ist
es doch evident, daſs z. B. die auf der Strecke Sagan-
Streckenblock gemessene Verzögerung von 30,4 Milliontel
Secunden anderen Ursprungs seyn muſs, als die auf
0,3 Milliontel Secunden berechnete Flaschenverzögerung.
Ich hoffe im Laufe dieses Winters Gelegenheit zu finden,
nicht nur die obigen Versuche unter besseren Verhältnissen
und mit verbesserten Vorrichtungen wiederholen, son-
dern sie auch auf eine Kupferleitung ausdehnen zu kön-
nen, um durch directe Messungen die Frage zu entscheiden,
ob die Geschwindigkeit der Elektricität von der
Natur des metallischen Leiters abhänge oder nicht. Nach
den mit dem metallischen Zinkvitriolösung gefüllten Kautschuk-
rohre angestellten Versuchen erscheint mir letzteres wahr-
scheinlich. Kirchhoff hat unter Zugrundelegung des
Weber’schen Fundamentalgesetzes für die Bewegung der
Elektricität die Zahl 41000 Meilen für die Geschwindigkeit
der Elektricität in Leitern durch Rechnung gefunden
und ist dabei zu dem Resultat gekommen, daſs diese Ge-
schwindigkeit gleich groſs in allen Leitern seyn müſse.
Unsere Messungen schlieſsen sich dem Kirchhoff’schen
Werthe wenigstens weit näher an, wie dem von Wheat-
stone aus dem Zurückbleiben des mittleren Funkens ge-
schätzten von 61900 geogr. Meilen.
Fizeau und Gounelle haben mit Hülfe ihrer Diffe-
rentialmeſsmethode für galvanische Ströme in Telegraphen-
leitungen für Kupfer 17792 Km., für Eisen 101710 Km.
gefunden, für Eisen also nur eine etwa halb so groſse Ge-
schwindigkeit wie unsere Messungen ergeben haben.
Poggendorff’s Annal. Bd. CLVII.
[Page 14]
21
Noch weit geringere Geschwindigkeitswerthe haben
Walker, Mitchell und Gould auf amerikanischen Tele-
graphenlinien mit elektromagnetischen Registrirapparaten
gefunden, letzterer sogar nur 12851 englische Meilen.
Auf diese Messungen ist jedoch kein groſses Gewicht zu
legen, da die Trägheit der elektromagnetischen Instrumente
zu groſs und ungleich für die Messung so kleiner Zeit-
theile ist. Von weit gröſserem Gewichte erscheinen die
Messungen von Fizeau und Gounelle. Dieselben haben den
verzögernden Einfluſs der Ladung, auf den ich erst nach An-
stellung ihrer Versuche aufmerksam machte, keine Rück-
sicht nehmen können und es fehlen in der Beschreibung
ihrer Versuche auch die nöthigen Data, um die Ladungs-
verzögerung nachträglich berechnen zu können. Wenn
aber auch die Ladungsverzögerung der verhältnismäſsig
groſsen Länge ihrer Leitung wegen (ca. 300 Km.) über
1000 mal gröſser wie bei meinen Versuchen seyn müſste,
so reicht sie doch zur Erklärung der Differenz noch nicht
aus. Ich glaube daher, daſs auch die von Fizeau ge-
fundene Verschiedenheit der Geschwindigkeit der Elek-
tricität in Eisen und Kupfer noch nicht als constatirt an-
zusehen ist.